
When you are playing a Backgammon match, whether or not to double, and whether or not to take, depends on many factors:
Estimating the odds of all but the last item is simply guesswork. And the more experience you have, the better your guesses will be. Experts can often estimate their winning odds within one or two percentage points. They are simply that good, and have so many "reference points" in their memory, that they can do this.
The last item, however, is not something that the expert players estimate... it is something they know. And they know the odds of winning or losing at every score because they have memorized the match equity tables and take points for every given score.
Let's assume you are in a position where you believe you will win the game 30 percent of the time. And your opponent has given you the cube, and you have to decide whether to take or drop. You should drop if your odds of winning the match are greater than 30 percent if you drop, and you should take if your odds of winning the match are less than 30 percent if you drop. You can't know if your odds are greater or less unless you know what your take point is.
You can learn Backgammon match equity and take points from books, by studying the tables, and you can also get help from computer programs that give you take points.
Let's look at the position below for example.
It is a match to 5, black leads 3-1, the cube is in the middle, and black is on roll. Black is trying to decide whether or not he should double, and if he does double, if white should take or drop. He knows he is winning this game, and he might even win a gammon, so maybe he should roll on. But if he doesn't double and wins the game, and only one point, he doesn't win the match. So he has a tough decision to make.

I put this position into a computer program called Snowie, and it tells us that black should not double. It also tells us that if doubled, white should take. The reason white should take is that he can redouble on the next roll, and whoever wins this game then wins the match. White has a better chance of winning the match if he takes this cube and redoubles than if he drops.
And the reason he has a better chance playing this game is because if he drops, he is only 18% to win the match, but he has well over 18% chance to win the game. In fact, as you can see below, according to Snowie, he wins this game 23% of the time. So he gains 5% by taking. And the reason he has a better chance playing this game is because if he drops, he is only 18% to win the match, but he has well over 18% chance to win the game. In fact, as you can see below, according to Snowie, he wins this game 23% of the time. So he gains 5% by taking.

I mentioned that the reason he knows he has 18% by dropping is by memorizing the take point and match equity tables. I also mentioned that you can get this information from the computer programs. In the case of Snowie, if you go to "Theory" and hit "sync" to get the table to apply to this particular situation, you will get the following screen.
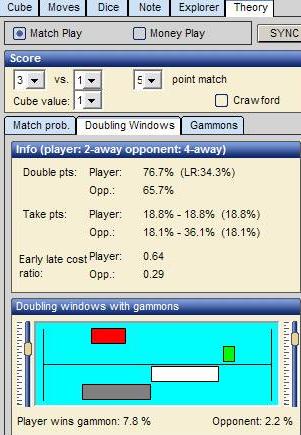
This screen tells you that the take point is 18.1% for white. So when he gets a cube like this, he knows that he should take if he thinks his odds are higher.
This is also helpful to black. He knows he should double if the takepoint for white is 18 percent but white's winning chances are less than 18%. In this case, since the winning odds are 23%, he should not double.
Does all this sound complicated to you? It did to me, for many years, and it took a lot of study, patience, memorization of tables, and coaching before I fully understood it, and I STILL HAVE PROBLEMS with these calculations from time to time. But I do not feel lonely, as everyone has some difficulty with this. Until you become a top player, you do not have to calculate these numbers exactly... you can estimate, as we all do to some extent. But you do need to understand the concept in order to estimate well.